第一章 单元测试

1、 问题:求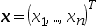,使其满足条件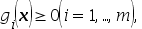并且使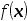到达最小，则该问题为（ ）.
选项：
A:约束极小化问题
B:约束极大化问题
C:无约束问题
答案: 【
约束极小化问题
】

2、 问题:根据决策变量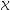取值类型，可以将最优化问题分为（ ）
选项：
A:凸优化问题和非凸优化问题
B:约束优化问题和无约束优化问题
C:连续优化问题和离散优化问题
答案: 【
连续优化问题和离散优化问题
】

3、 问题:若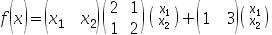,则=（ ）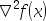
选项：
A: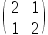
B: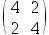
C: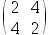
答案: 【

】

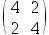
4、 问题:函数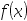在某点的梯度方向为函数在该点的（ ）
选项：
A:上升方向
B:下降方向
C:最速上升方向
答案: 【
最速上升方向
】

5、 问题:（ ）函数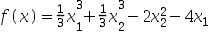的驻点。
选项：
A:(0,0)
B:(4,4)
C:(-2,4)
答案: 【
(-2,4)
】

6、 问题:在定义域内部可微函数的平稳点一定为极值点，反之未必。（ ）
选项：
A:正确
B:错误
C:不确定
答案: 【
错误
】

7、 问题:非空集合为凸集当且仅当D中任意有限个点的凸组合仍属于D.（ ）
选项：
A:正确
B:错误
C:不确定
答案: 【
正确
】

8、 问题:

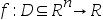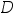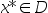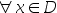设为凸集上的可微凸函数，，则对，有.（ ）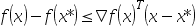

选项：
A:正确
B:错误
C:不确定
答案: 【
正确
】

9、 问题:若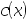是凹函数，则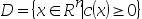是凸集.（ ）
选项：
A:正确
B:错误
C:不确定
答案: 【
正确
】

10、 问题:下列函数中是严格凸函数的为（ ）
选项：
A: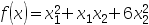
B: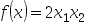
C: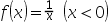
答案: 【

】

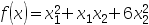
第二章 单元测试

1、 问题:对函数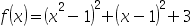，当给定搜索区间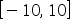，收敛精度为区间长度小于0.05，使用黄金分割法求得的近似解为（ ）
选项：
A:0.558
B:1.443
C:1.002
答案: 【
1.002
】

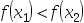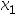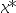2、 问题:使用黄金分割法时，初始区间为[a,b],若，则可去掉[a,]的部分，必在[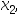b]内。（ ）
选项：
A:正确
B:错误
C:不确定
答案: 【
错误
】

3、 问题:

用0.618法求函数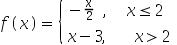在区间[0,3]上的极小点时，第一次消去时去掉的哪个区间（ ）。

选项：
A: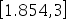
B: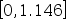
C: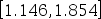
答案: 【

】

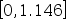
4、 问题:在使用黄金分割法迭代运算时，迭代区间不断缩小，其区间缩小率在迭代过程中（ ）
选项：
A:逐步变小
B:不变
C:逐步变大
答案: 【
不变
】

5、 问题:抛物线逼近法必须先求出满足“两头大、中间小”的三个初始点。（ ）
选项：
A:正确
B:错误
C:不确定
答案: 【
正确
】

6、 问题:抛物线逼近法不需要迭代过程。（ ）
选项：
A:正确
B:错误
C:不确定
答案: 【
错误
】

7、 问题:使用抛物线法求min 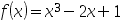的近似最优解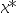为（ ），其中初始搜索区间为[0,3]，区间精度取0.01。
选项：
A:-0.0879
B:1.0
C:0.8165
答案: 【
0.8165
】

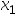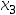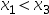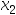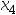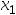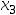8、 问题:在单谷区间[,]（）中，取一点，用三点二次插值法计算得（在[,]内），若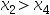，并且其函数值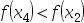，则取新区间为（ ）
选项：
A:[,]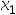
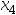B:[,]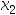
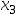C:[,]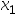
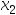答案: 【
[,]
】

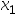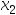9、 问题:用外推内插法确定一维极小化问题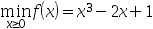的搜索区间为（ ），要求选取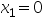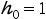，，步长加步倍数为2。
选项：
A:[0,2]
B:[-1,-1]
C:[-2,2]
答案: 【
[0,2]
】

10、 问题:用外推内插法确定一维最小化问题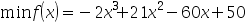的搜索区间为（ ），要求选取初始点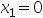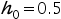，，步长加步倍数为2。
选项：
A:[-3,3]
B:[1.5,3.5]
C:[2,8]
答案: 【
[1.5,3.5]
】

第三章 单元测试

1、 问题:用变量轮换法求函数的极小点，初始点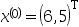，当满足时，迭代点为（ ）
选项：
A:(7.875,5.9375)
B:(7.5,5.75)
C:(7.5,5)
答案: 【
(7.875,5.9375)
】

本门课程剩余章节答案为付费内容
本文章不含期末不含主观题！！
本文章不含期末不含主观题！！
支付后可长期查看
有疑问请添加客服QQ 2356025045反馈
如遇卡顿看不了请换个浏览器即可打开
请看清楚了再购买哦，电子资源购买后不支持退款哦
点我支付 ¥5
  已支付？输入手机号或商家订单号阅读