2022知到答案 组合优化 最新完整智慧树知到满分章节测试答案
第一章 单元测试
1、 问题:设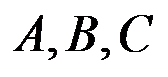 是欧氏平面上三个点,连接这三个点的最小Steiner树长度必小于这三个点形成的赋权完全图的最小生成树长度。( )
是欧氏平面上三个点,连接这三个点的最小Steiner树长度必小于这三个点形成的赋权完全图的最小生成树长度。( )
选项:
A:对
B:错
答案: 【
错
】
2、 问题:以下对背包问题最优解的描述,正确的是( )
选项:
A:对于连续形式的背包问题,最优解中放入背包的物品大小之和为背包的容量。
B:对于离散形式的背包问题,最优解中放入背包的物品大小之和为背包的容量。
C:对于连续形式的背包问题,放入背包的物品大小之和为背包容量的解必为最优解。
D:对于离散形式的背包问题,放入背包的物品大小之和为背包容量的解必为最优解。
答案: 【
对于连续形式的背包问题,最优解中放入背包的物品大小之和为背包的容量。
】
3、 问题:
考虑下面的批排序问题。若干个工件需在一台批处理机上加工,工件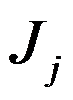 的大小为
的大小为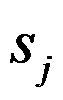 。大小之和不超过
。大小之和不超过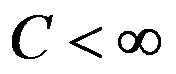 的若干个工件可作为一批同时加工,每批的加工时间均相等。工件的完工时间定义为它所在批的完工时间,目标为极小化工件最大完工时间。与该问题等价的问题是( )。
的若干个工件可作为一批同时加工,每批的加工时间均相等。工件的完工时间定义为它所在批的完工时间,目标为极小化工件最大完工时间。与该问题等价的问题是( )。
选项:
A: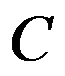 台机器的平行机排序问题
台机器的平行机排序问题
B:箱容量为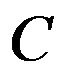 的一维装箱问题
的一维装箱问题
C:背包容量为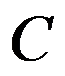 的背包问题
的背包问题
D:其他选项都不对
答案: 【
箱容量为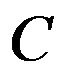 的一维装箱问题
的一维装箱问题
】
4、 问题:以下字符集,不能作为字母表的是( )。
选项:
A: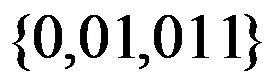
B: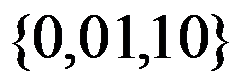
C: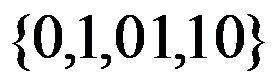
D: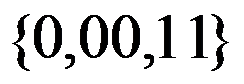
答案: 【
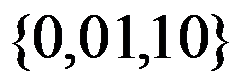
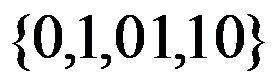
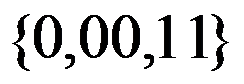
】
5、 问题:考虑单台机排序问题,工件集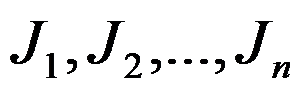 依次在一机器上加工,机器在同一时间只能加工一个工件,工件
依次在一机器上加工,机器在同一时间只能加工一个工件,工件 的加工时间为
的加工时间为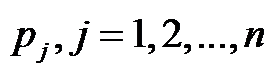 ,则所有工件的完工时间之和为( )。
,则所有工件的完工时间之和为( )。
选项:
A: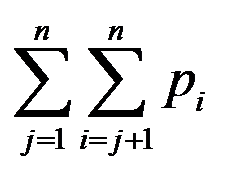
B: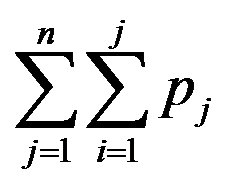
C: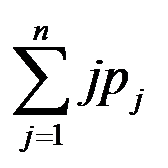
D: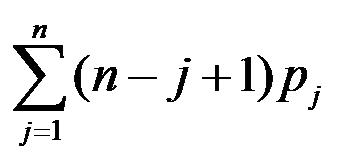
答案: 【
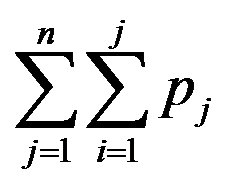
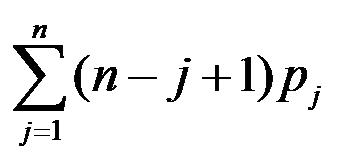
】
第二章 单元测试
1、 问题:若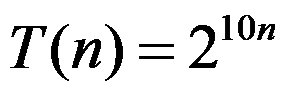 ,则
,则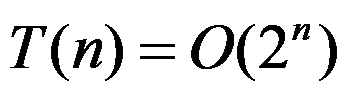 。 ( )
。 ( )
选项:
A:对
B:错
答案: 【
错
】
2、 问题:设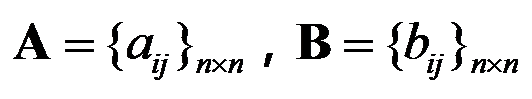 为
为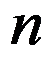 阶方阵。现用以下算法求
阶方阵。现用以下算法求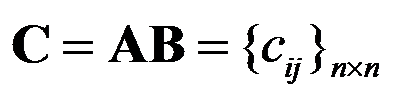 。
。
算法:
For i = 1 to n do
For j = 1 to n do
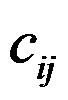 = 0
= 0
For k = 1 to n do
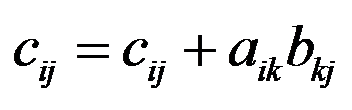
输出
该算法的时间复杂度为( )。
选项:
A: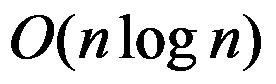
B: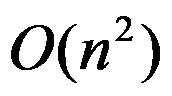
C: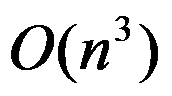
D: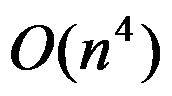
答案: 【
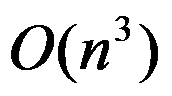
】
3、 问题:若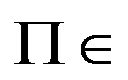 NP,以下能说明
NP,以下能说明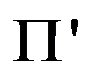 是NP-C问题的是( )。
是NP-C问题的是( )。
选项:
A:对任意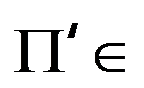 NP,
NP,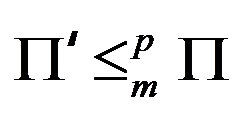 。
。
B:存在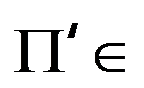 NP,
NP,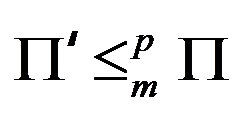 。
。
C:对任意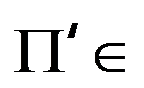 NP-C,
NP-C,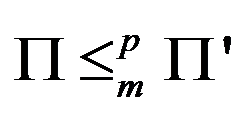 。
。
D:存在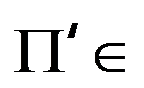 NP-C,
NP-C,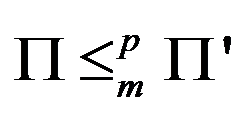 。
。
答案: 【
对任意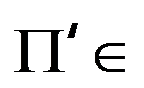 NP,
NP,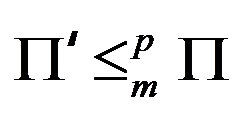 。
。
】
4、 问题:设有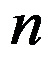 个城市的TSP问题实例,城市之间距离为
个城市的TSP问题实例,城市之间距离为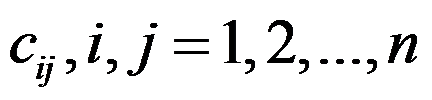 ,以下是该实例规模合理表达式的有( )。
,以下是该实例规模合理表达式的有( )。
选项:
A: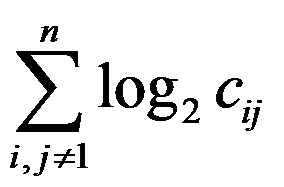
B: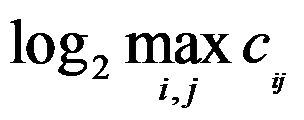
C: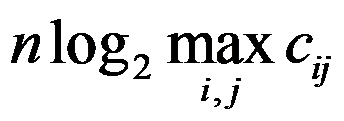
D: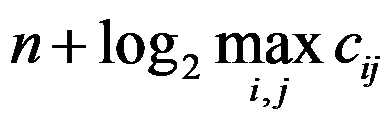
答案: 【
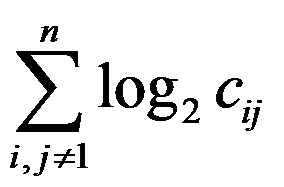
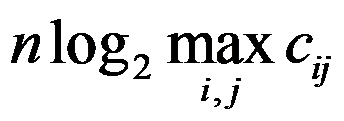
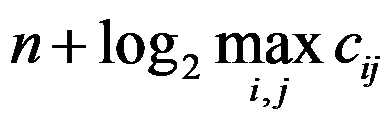
】
5、 问题:设一平行机排序问题算法的时间复杂度为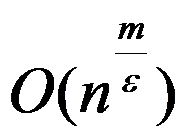 ,其中
,其中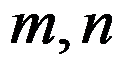 分别为机器数和工件数,
分别为机器数和工件数,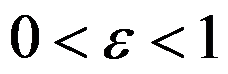 为一与实例无关的常数。以下说法准确的有( )。
为一与实例无关的常数。以下说法准确的有( )。
选项:
A:若在该问题中,机器数是一个固定常数,该算法是一个多项式时间算法。
B:若在该问题中,机器数是一个固定常数,该算法是一个指数时间算法。
C:若在该问题中,机器数可能随实例不同而变化,该算法是一个多项式时间算法。
D:若在该问题中,机器数可能随实例不同而变化,该算法是一个指数时间算法。
答案: 【
若在该问题中,机器数是一个固定常数,该算法是一个多项式时间算法。
若在该问题中,机器数可能随实例不同而变化,该算法是一个指数时间算法。
】
第三章 单元测试
1、 问题:设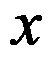 是取值在
是取值在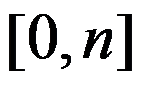 中的整变量,
中的整变量,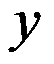 为0-1变量,“
为0-1变量,“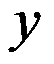 取值为1当且仅当
取值为1当且仅当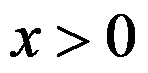 ”可用
”可用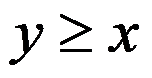 来表示。( )
来表示。( )
选项:
A:对
B:错
答案: 【
错
】
本文章不含期末不含主观题!!
本文章不含期末不含主观题!!
支付后可长期查看
有疑问请添加客服QQ 2356025045反馈
如遇卡顿看不了请换个浏览器即可打开
请看清楚了再购买哦,电子资源购买后不支持退款哦


