2022知到答案 运筹学（物流工程微专业） 最新完整智慧树知到满分章节测试答案

绪论 单元测试

1、 问题:运筹学的主要研究内容有（ ）
选项：
A:运用分析理论
B:竞争理论
C:随机服务理论即排队论
D:不确定性理论
答案: 【
运用分析理论
竞争理论
随机服务理论即排队论
】

第一章 单元测试

1、 问题:关于线性规划模型的可行域，下面（ ）的叙述是正确的。
选项：
A:可行域内必有无穷多个点
B:可行域必有界
C:可行域内必然包括原点
D:可行域必是凸集
答案: 【
可行域必是凸集
】

2、 问题:图解法适用于（ ）个变量的线性规划问题
选项：
A:1
B:2
C:3
D:4
答案: 【
2
3
】

3、 问题:线性规划问题是针对（ ）求极值问题。
选项：
A:约束
B:决策变量
C:目标函数
D:可行域
答案: 【
目标函数
】

4、 问题:若可行域有界，线性规划问题的目标函数一定在可行域的顶点上达到最优。（ ）
选项：
A:对
B:错
答案: 【
对
】

5、 问题:线性规划的相关假设包括（ ）。
选项：
A:比例性假设
B:可加性假设
C:可分性假设
D:确定性假设
答案: 【
比例性假设
可加性假设
可分性假设
确定性假设
】

6、 问题:在线性规划建模时，决策变量并不要求必须在等号或不等号的左侧。（ ）
选项：
A:对
B:错
答案: 【
对
】

7、 问题:以下形式正确表示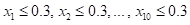是（ ）。
选项：
A: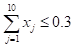
B: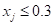
C: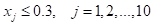
D: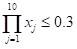
答案: 【

】

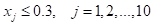
8、 问题:在单纯形法计算过程中，将某个非基变量变为基变量的作用是：一个基可行解沿约束边界向相邻基可行解移动。（ ）
选项：
A:对
B:错
答案: 【
对
】

9、 问题:关于线性规划问题解的描述，说法正确的有（ ）。
选项：
A:可行解包括基本可行解；
B:基本可行解对应的是可行域的顶点；
C:若该问题有n个决策变量，则角点解对应于n个约束边界的交点；
D:满足约束条件的基解称为基可行解。
答案: 【
可行解包括基本可行解；
基本可行解对应的是可行域的顶点；
若该问题有n个决策变量，则角点解对应于n个约束边界的交点；
满足约束条件的基解称为基可行解。
】

10、 问题: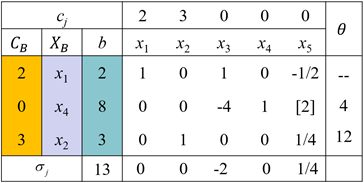
10、 根据以下单纯形表，换出变量为（ ）。
选项：
A: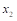
B: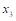
C: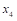
D: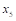
答案: 【

】

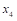
11、 问题:基矩阵一定是非奇异的。（ ）
选项：
A:对
B:错
答案: 【
对
】

12、 问题:利用单纯形法求解最大化线性规划模型时，当前解为最优解的判别依据为（ ）。
选项：
A:当前解X是基本解；
B:当前解X是基本可行解；
C:非基变量的检验数为非正；
D:基变量的检验数为非正。
答案: 【
当前解X是基本可行解；
非基变量的检验数为非正；
】

13、 问题: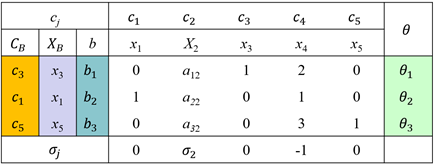
13、 对于最大化线性规划问题，最终单纯形表如下所示，若为无界解，则需满足（ ）。
选项：
A: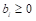
B: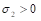
C: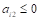
D: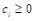
答案: 【



】

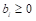
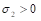
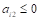
14、 问题:利用单纯形法求解线性规划问题时，若在最终单纯形表中人工变量未退出基变量，则该问题无可行解。（ ）
选项：
A:对
B:错
答案: 【
对
】

15、 问题:对于最大化线性规划问题，无穷多最优解的判定条件包括（ ）。
选项：
A:当前解是基本可行解；
B:非基变量的检验数满足最优性检验；
C:存在某个非基变量的检验数等于0；
D:存在某个非基变量的检验数大于0。
答案: 【
当前解是基本可行解；
非基变量的检验数满足最优性检验；
存在某个非基变量的检验数等于0；
】

第二章 单元测试

1、 问题:无论原线性规划问题是最大化问题还是最小化问题，当其变量为无约束时，其对偶问题对应的约束条件均为“=”。（ ）
选项：
A:对
B:错
答案: 【
对
】

2、 问题:利用单纯形法求解线性规划问题时，基变量的检验数一定是0。（ ）
选项：
A:对
B:错
答案: 【
对
】

3、 问题:原线性规划问题为最大化问题，该问题的约束条件为“=”，则其对偶问题对应的变量（ ）。
选项：
A:≥0
B:≤0
C:=0
D:无约束
答案: 【
无约束
】

4、 问题: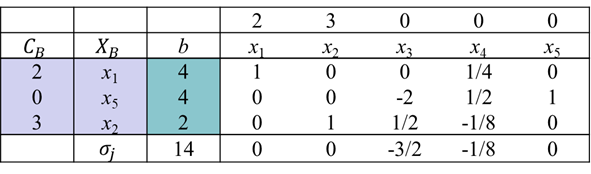
4、 根据以下某步单纯形表，当前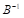为（ ）。
选项：
A: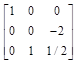
B: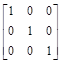
C: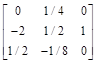
D: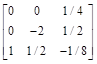
答案: 【

】

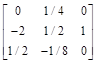
5、 问题:松弛变量可以作为基变量，但不能作为非基变量。（ ）
选项：
A:对
B:错
答案: 【
错
】

6、 问题:利用单纯形法求解线性规划问题时，剩余变量对应的检验数计算公式为 。（ ）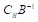
选项：
A:对
B:错
答案: 【
对
】

7、 问题:线性规划问题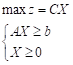的对偶问题为（ ）。
选项：
A: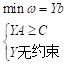
B: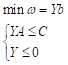
C: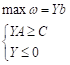
D: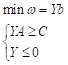
答案: 【

】

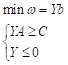
8、 问题:在对偶单纯形法求解中，若换出变量对应的系数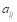都大于0，则该问题解的情况为（ ）
选项：
A:有无穷多最优解
B:有唯一最优解
C:无界解
D:无可行解
答案: 【
无可行解
】

9、 问题:“在线性规划问题的最优解中，如果对应某一约束条件的对偶变量值为非零，则该约束条件取严格等式；反之如果约束条件取严格不等式，则其对应的对偶变量一定为零。”该性质是根据对偶基本性质中的哪条性质推导得到的？（ ）。
选项：
A:对称性
B:弱对偶性
C:强对偶性
D:互补松弛性
答案: 【
互补松弛性
】

10、 问题:对偶单纯形法是用于求解对偶问题的方法 （ ）
选项：
A:对
B:错
答案: 【
错
】

11、 问题:最小化问题（对偶问题）的任一可行解对应的目标函数值是原问题最优目标函数的下界。（ ）
选项：
A:对
B:错
答案: 【
错
】

12、 问题:若原问题为“目标函数最小化、结构约束为大于等于约束、决策变量非负”的形式，则剩余变量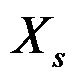对应的检验数计算公式为（ ）。
选项：
A: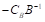
B: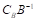
C:0
D: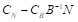
答案: 【

】

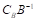
13、 问题:若原问题是大化问题，则以下关于单纯形法和对偶单纯形法的描述，正确的有（ ）
选项：
A:对偶单纯形法关注的是不可行的角点解，其求解过程始终要求对偶问题的解满足可行性。
B:对偶单纯形法是用于求解对偶问题的一种算法。
C:对偶单纯形法的换基顺序为：先确定换入变量，再确定换出变量。
D:对偶单纯形法是单纯形法的一种镜像，它对应于用单纯形法求解对偶问题的过程。
答案: 【
对偶单纯形法关注的是不可行的角点解，其求解过程始终要求对偶问题的解满足可行性。
对偶单纯形法是单纯形法的一种镜像，它对应于用单纯形法求解对偶问题的过程。
】

14、 问题:若原问题有可行解，但其目标函数值无界，则对偶问题目标函数值无界。（ ）
选项：
A:对
B:错
答案: 【
错
】

15、 问题: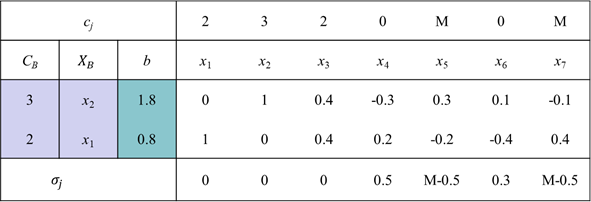
15、 根据以下某步单纯形表，当前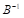为（ ）。
选项：
A: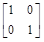
B: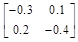
C: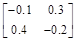
D: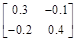
答案: 【

】

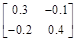
第三章 单元测试

1、 问题:在运输问题中，可以作为表上作业法的初始基可行解的调运方案应满足的条件是（ ）。
选项：
A:含有m+n-1个基变量
B:基变量不构成闭回路
C:含有m+n-1个基变量且不构成闭回路
D:含有m+n-1个非零的基变量且不构成闭回
答案: 【
含有m+n-1个非零的基变量且不构成闭回
】