2022知到答案 高等数学挑战 最新完整智慧树知到满分章节测试答案
绪论 单元测试
1、 问题:下列命题不正确的是( )
选项:
A:设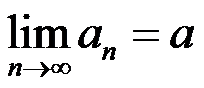 ,则
,则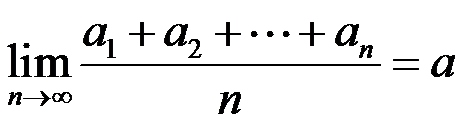
B:设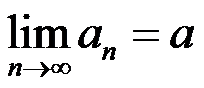 ,
, ,则
,则
C:设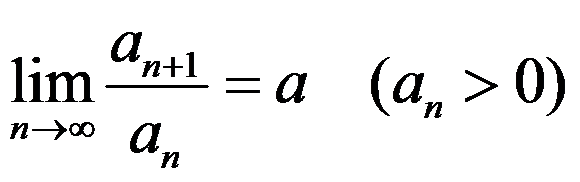 ,则
,则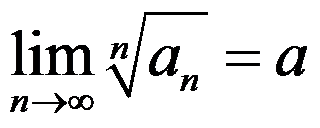
D: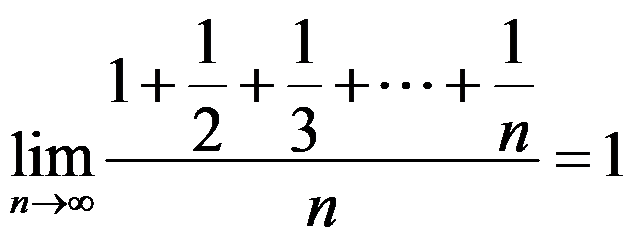
答案: 【
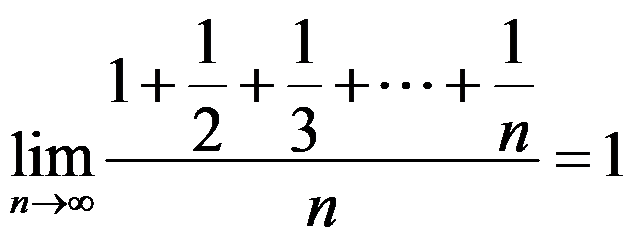
】
2、 问题:设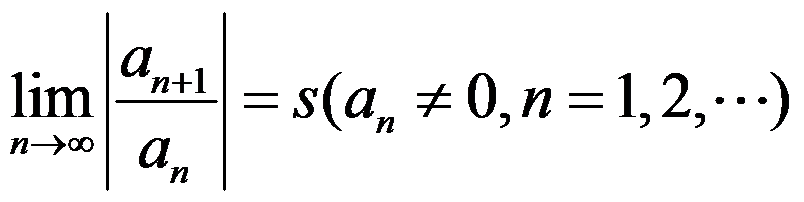 ,则( )
,则( )
选项:
A: 时,
时, 为无穷大数列
为无穷大数列
B: 为无穷大数列时,
为无穷大数列时,
C: 时,
时, 为无界数列
为无界数列
D: 为无界数列时,
为无界数列时,
答案: 【
 时,
时, 为无穷大数列
为无穷大数列
】
3、 问题:若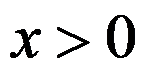 ,则由拉格朗日中值定理,
,则由拉格朗日中值定理,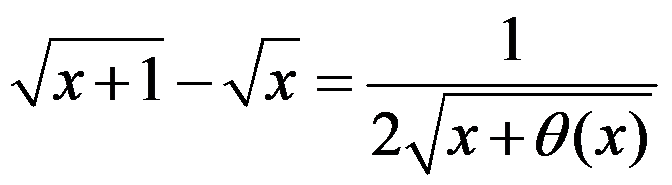 ,其中( )
,其中( )
选项:
A: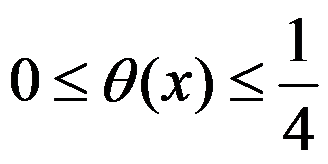
B: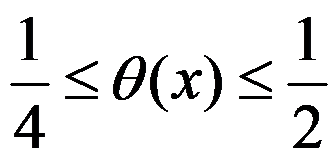
C: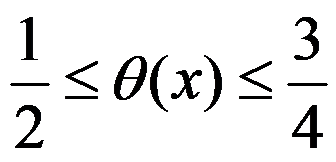
D: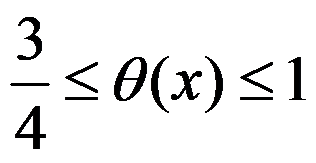
答案: 【
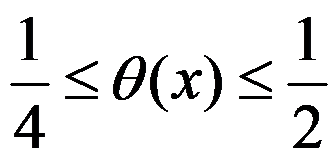
】
4、 问题:设函数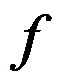 在
在 上连续,在
上连续,在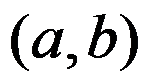 内可导,且
内可导,且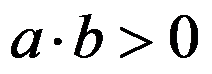 ,则存在
,则存在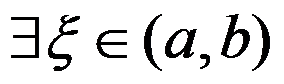 ,使得( )
,使得( )
选项:
A: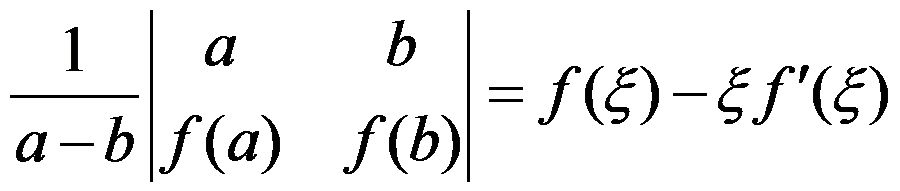
B:
C: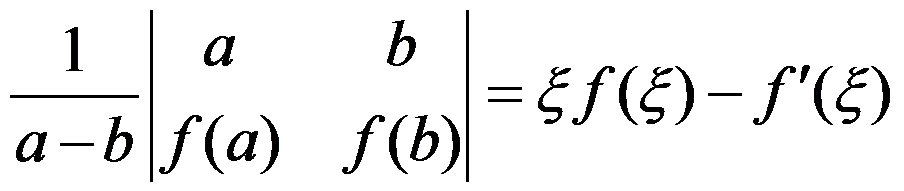
D: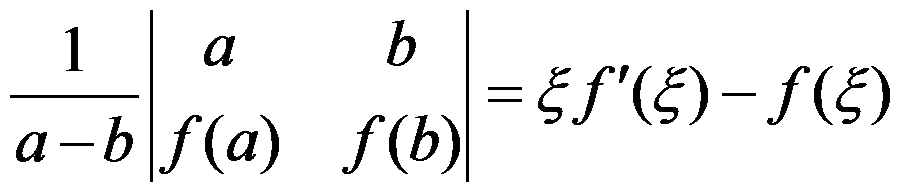
答案: 【
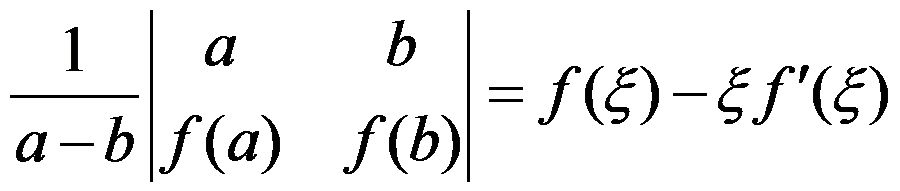
】
5、 问题:设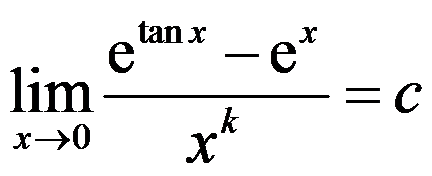 ,
, 为非零常数,则( )
为非零常数,则( )
选项:
A: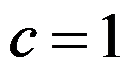
B: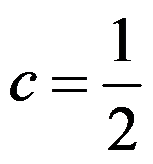
C: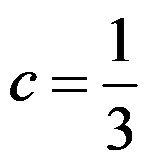
D: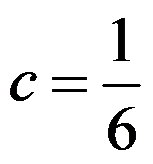
答案: 【
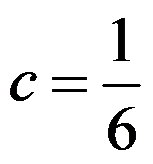
】
6、 问题:设 在区间
在区间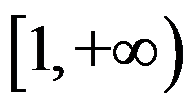 上可导,下列结论中成立的是( )
上可导,下列结论中成立的是( )
选项:
A:若 ,则
,则 在区间
在区间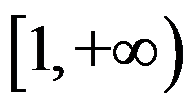 上有界
上有界
B:若 ,则
,则 在区间
在区间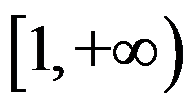 上无界
上无界
C:若 ,则
,则 在区间
在区间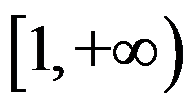 上无界
上无界
D:若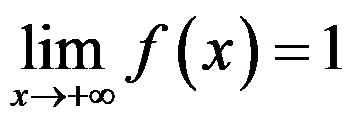 ,则
,则 在区间
在区间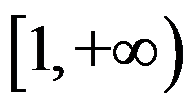 上无界
上无界
答案: 【
若 ,则
,则 在区间
在区间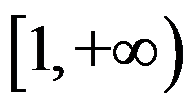 上无界
上无界
】
7、 问题:设由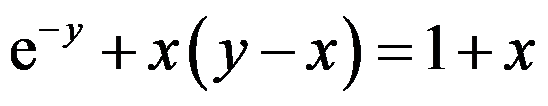 确定函数
确定函数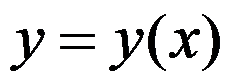 ,则
,则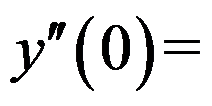 ( )
( )
选项:
A:
B: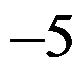
C: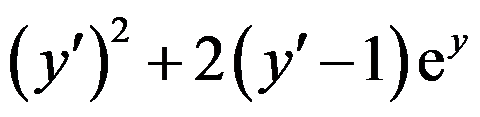
D:
答案: 【
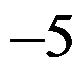
】
8、 问题:设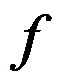 在区间
在区间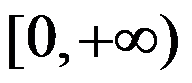 上可微,且
上可微,且 ,则在
,则在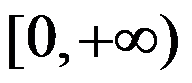 上( )
上( )
选项:
A: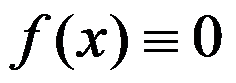
B: 单调递增
单调递增
C: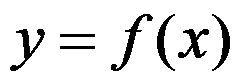 可能凸,也可能凹
可能凸,也可能凹
D:没有正根
【提示】令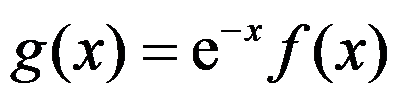 ,则
,则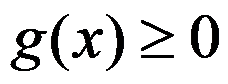 ;又因
;又因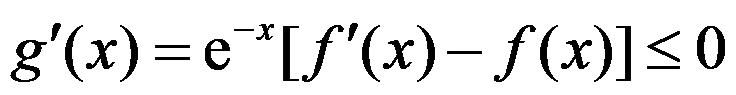 ,故
,故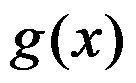 递减,
递减, ,故
,故 ,从而
,从而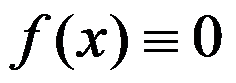 .
.
答案: 【
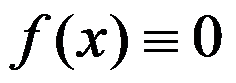
】
9、 问题:
计算: ( )
( )
选项:
A:
B: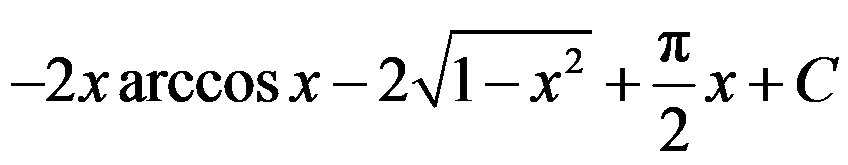
C: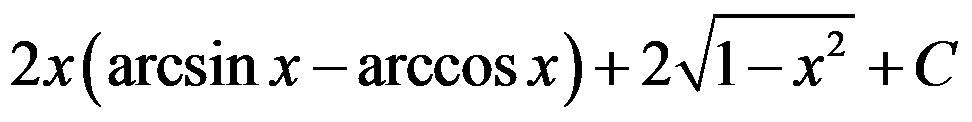
D:
答案: 【

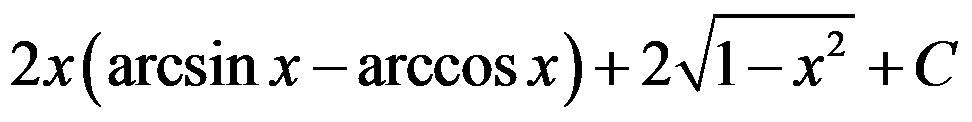
】
10、 问题:设 在区间
在区间 上连续,单调递减,为使
上连续,单调递减,为使 成立,
成立, 应满足( )
应满足( )
选项:
A: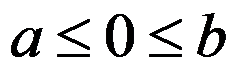
B:
C: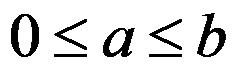
D: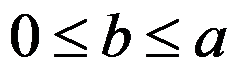
答案: 【
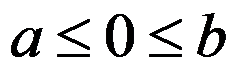
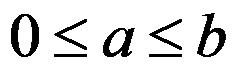
】
第一章 单元测试
1、 问题:
计算此式: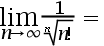 ( )
( )
选项:
A:
B:
C:
D: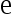
答案: 【

】
2、 问题:
求此式子: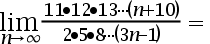 ( )
( )
选项:
A:
B:
C:
D: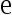
答案: 【

】
3、 问题:已知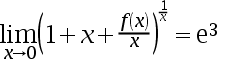 , 则
, 则 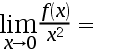 ( )
( )
选项:
A:
B:
C:
D:
答案: 【

】
4、 问题:以下极限数值最小的那个是( )
选项:
A: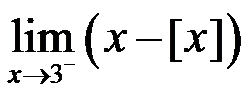
B: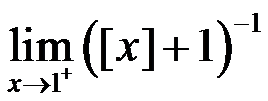
C: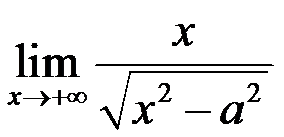
D: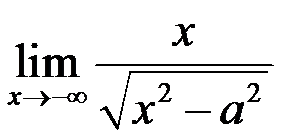
答案: 【
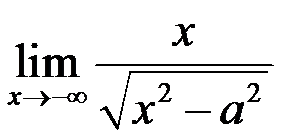
】
5、 问题:下列极限计算错误的是( )
选项:
A: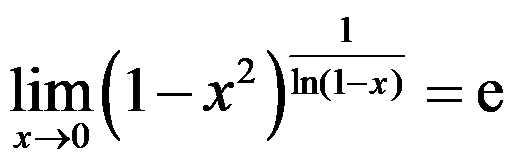
B: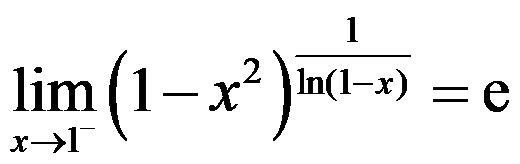
C:
D: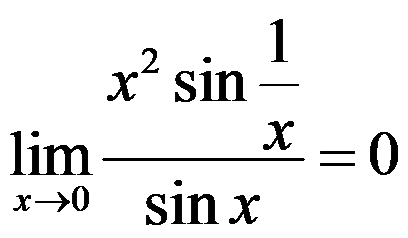
答案: 【
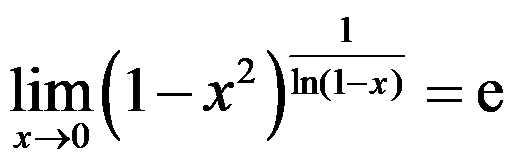
】
6、 问题:
求解: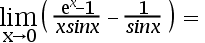 ( )
( )
选项:
A:
B:
C: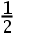
D:
答案: 【
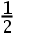
】
7、 问题:
此式子: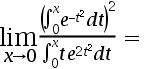 ( )
( )
选项:
A:
B:
C:
D: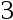
答案: 【

】
8、 问题:下列命题正确的是( )
选项:
A: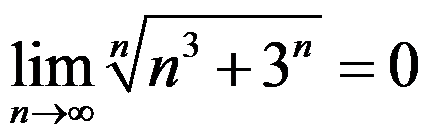
B: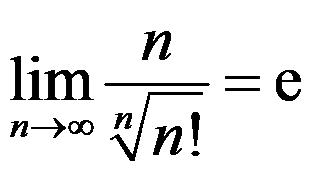
C: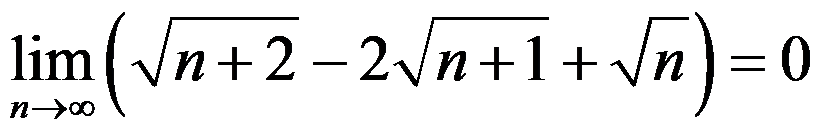
D: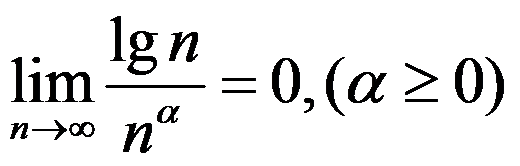
答案: 【
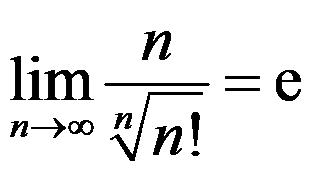
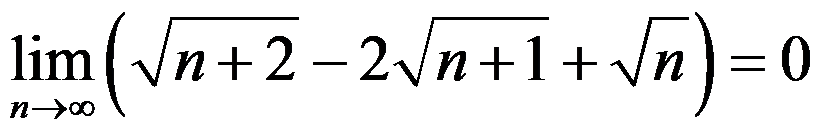
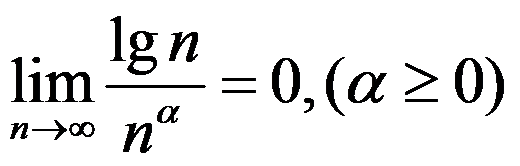
】
9、 问题:设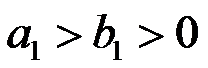 ,记
,记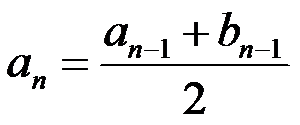 ,
, ,
, ,则( )
,则( )
选项:
A:数列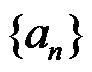 单调递减
单调递减
B:数列 单调递增
单调递增
C:
D: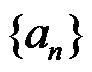 的极限为
的极限为 ,
, 的极限为
的极限为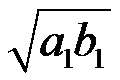
答案: 【
数列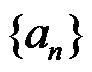 单调递减
单调递减
数列 单调递增
单调递增

】
第二章 单元测试
1、 问题:设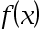 可导,
可导, 欲使
欲使 在
在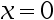 可导,则必有( ).
可导,则必有( ).
选项:
A: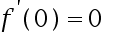
B: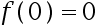
C: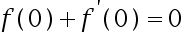
D: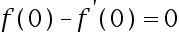
答案: 【
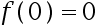
】
2、 问题:若函数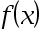 在
在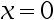 处连续,且
处连续,且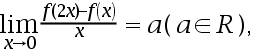 则
则 ( ).
( ).
选项:
A: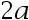
B: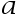
C:0
D:不存在
答案: 【
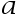
】
3、 问题:设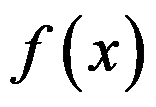 在
在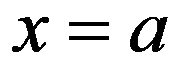 处可导,且
处可导,且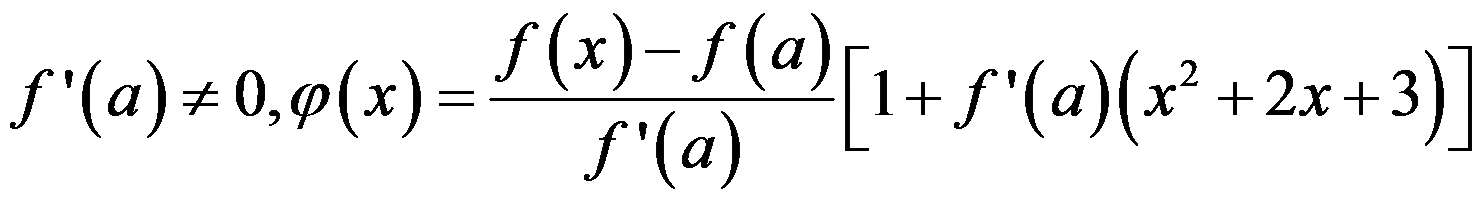 ,则
,则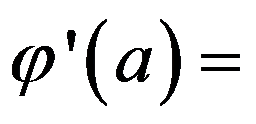 ( ).
( ).
选项:
A: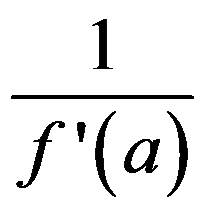
B: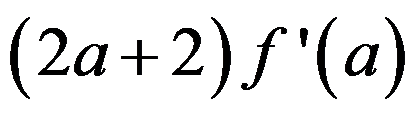
C:
D:
答案: 【

】
4、 问题:已知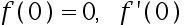 存在,则
存在,则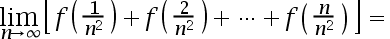 ( ).
( ).
选项:
A:0
B:
C: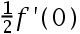
D:
答案: 【
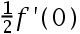
】
5、 问题:设函数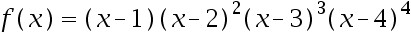 ,则
,则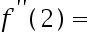 ( ).
( ).
选项:
A: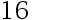
B:
C:
D: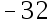
答案: 【
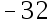
】
6、 问题:设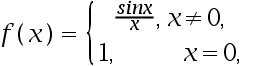 则
则 ( ).
( ).
选项:
A: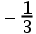
B: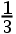
C:0
D: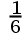
答案: 【
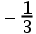
】
7、 问题:若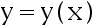 由方程组
由方程组 确定,则
确定,则 ( ).
( ).
选项:
A: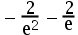
B: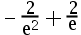
C: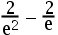
D:
答案: 【
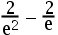
】
8、 问题:设当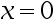 时
时 则
则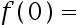 ( ).
( ).
选项:
A:1
B: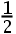
C: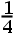
D:0
答案: 【
】
9、 问题:对函数 ,下列说法正确的是( )
,下列说法正确的是( )
选项:
A:该函数的解析式为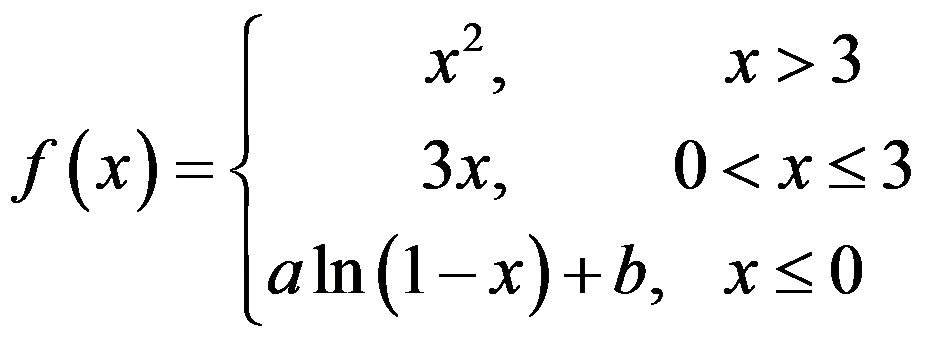
B:若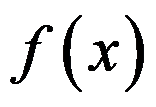 在
在 处连续
处连续
C:若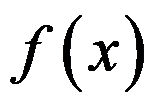 在
在 处可导
处可导
D:若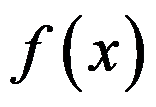 在
在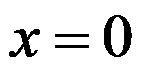 处可导,则
处可导,则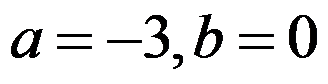
答案: 【
该函数的解析式为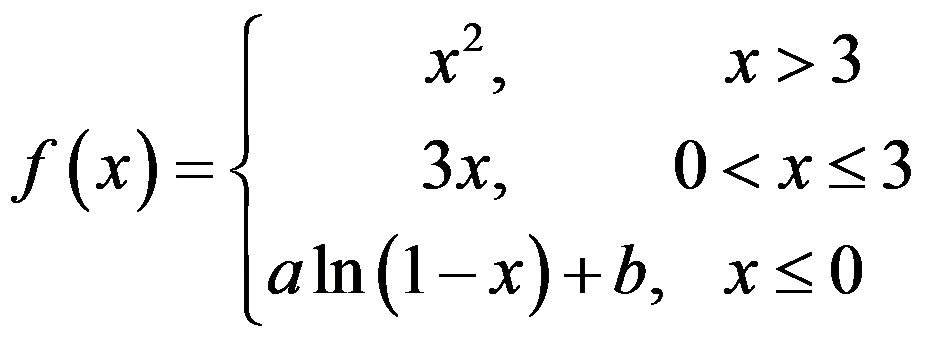
若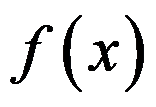 在
在 处连续
处连续
若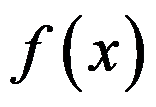 在
在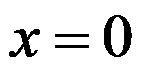 处可导,则
处可导,则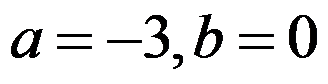
】
10、 问题:下列关于函数连续性或可导性的判断正确的是( )
选项:
A: 在
在 处均连续、不可导
处均连续、不可导
B: 在
在 上有定义且恒有
上有定义且恒有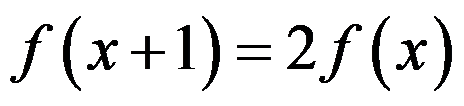 , 当
, 当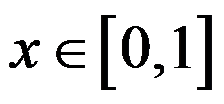 时
时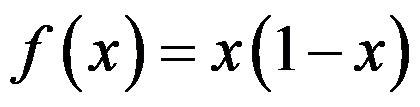 ,则
,则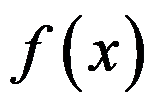 在
在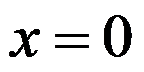 处可导
处可导
C: 在
在 处可导且
处可导且
D: 在
在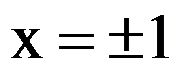 均不可导
均不可导
答案: 【
 在
在 处均连续、不可导
处均连续、不可导
 在
在 处可导且
处可导且
 在
在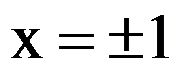 均不可导
均不可导
】
第三章 单元测试
1、 问题:
假设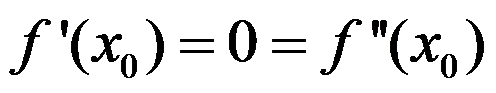 ,
,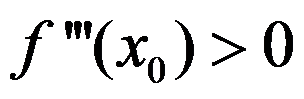 ,则( )
,则( )
选项:
A:.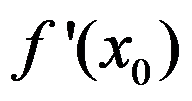 是
是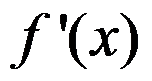 的极大值
的极大值
B:.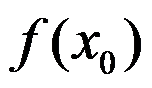 是
是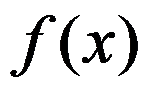 的极大值
的极大值
C:. 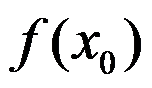 是
是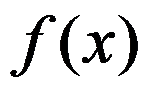 的极小值
的极小值
D:. 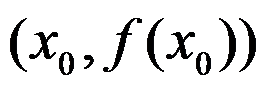 是曲线
是曲线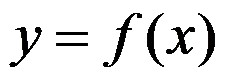 的拐点
的拐点
答案: 【
. 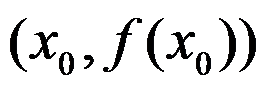 是曲线
是曲线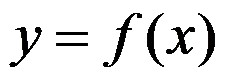 的拐点
的拐点
】
本文章不含期末不含主观题!!
本文章不含期末不含主观题!!
支付后可长期查看
有疑问请添加客服QQ 2356025045反馈
如遇卡顿看不了请换个浏览器即可打开
请看清楚了再购买哦,电子资源购买后不支持退款哦


