2020 高等数学(下)(西华大学)1207033214 最新满分章节测试答案
- 【作业】第七章 常微分方程 微分方程单元作业
- 第七章 常微分方程 微分单元测试题
- 【作业】第八章 向量代数与空间解析几何 向量代数与空间解析几何单元作业
- 第八章 向量代数与空间解析几何 向量代数与空间解析几何单元测试题
- 【作业】第九章 多元函数微分法及其应用 多元函数微分学单元作业
- 第九章 多元函数微分法及其应用 多元函数微分学单元测试题
- 第十章 重积分 重积分单元测验
- 【作业】第十章 重积分 重积分单元作业
- 第十一章 曲线积分与曲面积分 第十一章单元测验
- 【作业】第十一章 曲线积分与曲面积分 第十一章单元作业
- 【作业】第十二章 无穷级数 无穷级数单元作业
- 第十二章 无穷级数 无穷级数单元测验
- 【作业】第七章 常微分方程 微分方程(第三期开课)单元作业题
- 第七章 常微分方程 微分方程第三期单元测试题
- 【作业】第八章 向量代数与空间解析几何 向量代数与空间解析几何(第三期开课)单元作业题
- 第八章 向量代数与空间解析几何 向量代数与空间解析几何(第三期开课)单元测试题
- 【作业】第九章 多元函数微分法及其应用 多元函数微分学(第三期开课)单元作业题
- 【作业】第十章 重积分 重积分(第三期开课)单元作业题
- 第十章 重积分 重积分(第三期开课)单元测试题
- 第十一章 曲线积分与曲面积分 曲线微分与曲面积分(第三期开课)单元测试题
本答案对应课程为:点我自动跳转查看
本课程起止时间为:2020-02-24到2020-06-30
本篇答案更新状态:已完结
【作业】第七章 常微分方程 微分方程单元作业
1、 问题:函数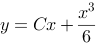 (其中C是任意常数)对微分方程
(其中C是任意常数)对微分方程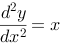 而言,是否是解,若是解,是通解吗?
而言,是否是解,若是解,是通解吗?
评分规则: 【 因为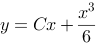 满足方程
满足方程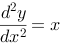 ,故是解
,故是解
但由于微分方程是二阶的,但所给解中所含不能合并的任意常数的个数是一个,故不是通解.
】
2、 问题:求方程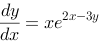 的通解.
的通解.
评分规则: 【 分离变量为:
所以通解为: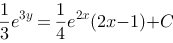
】
3、 问题:函数 是某微分方程的通解,求此微分方程.
是某微分方程的通解,求此微分方程.
评分规则: 【 因为 ,所以所以
,所以所以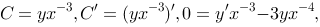
所以所求微分方程为: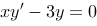
】
4、 问题:求微分方程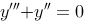 的通解
的通解
评分规则: 【 因为特征方程是: ,所以特征根中:
,所以特征根中: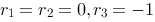 ,
,
故微分方程的通解是: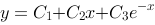
】
5、 问题:设二阶线性微分方程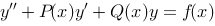 有三个特解分别为:
有三个特解分别为: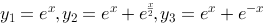 ,求此微分方程.
,求此微分方程.
评分规则: 【 因为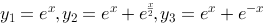 是二阶非齐次微分方程的三个解,所以
是二阶非齐次微分方程的三个解,所以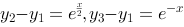 是二阶非齐次微分方程所对应的齐次微分方程的两个解,故二阶齐次微分方程的两个特征根分别是:
是二阶非齐次微分方程所对应的齐次微分方程的两个解,故二阶齐次微分方程的两个特征根分别是: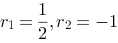
将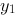 代入二阶非齐次微分方程中,求得
代入二阶非齐次微分方程中,求得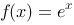
所求微分方程为:
】
6、 问题:求微分方程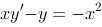 的通解.
的通解.
评分规则: 【 因为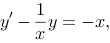 ,所以
,所以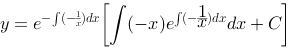
所以通解为: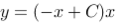
】
7、 问题:求微分方程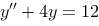 的通解.
的通解.
评分规则: 【 特征方程为: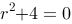 特征根为:
特征根为: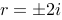 特解为:
特解为: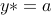
所以通解为: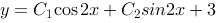
】
8、 问题:求微分方程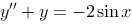 的通解.
的通解.
评分规则: 【 特征方程为: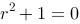 特征根为:
特征根为: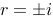 特解为:
特解为: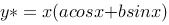
所以通解为: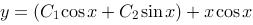
】
9、 问题:求微分方程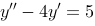 满足初值条件
满足初值条件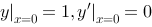 的特解 .
的特解 .
评分规则: 【 方程的通解为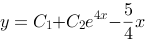 ,
,
特解为: .
.
】
10、 问题:设对任意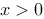 ,曲线
,曲线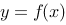 上点
上点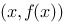 处的切线在
处的切线在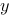 轴上截距等于
轴上截距等于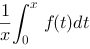 ,求
,求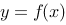 的一般表达式.
的一般表达式.
评分规则: 【 切线方程为: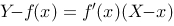 在
在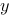 轴上截距:
轴上截距:
根据题意建立的方程为: ,两边求导,化简得
,两边求导,化简得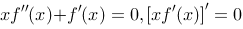
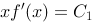 因此
因此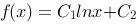 .
.
】
第七章 常微分方程 微分单元测试题
1、 问题:函数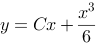 (其中C为任意常数)对微分方程
(其中C为任意常数)对微分方程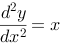 而言,( )
而言,( )
选项:
A:是通解
B:是特解
C:是解,但既非通解也非特解
D:不是解
答案: 【是解,但既非通解也非特解】
2、 问题:微分方程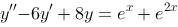 r的一个特解应具有形式(其中
r的一个特解应具有形式(其中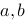 为常数)( )
为常数)( )
选项:
A: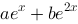
B: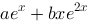
C: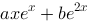

D: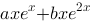
答案: 【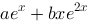 】
】
3、 问题:设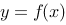 是微分方程
是微分方程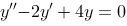 的一个解,若
的一个解,若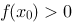 ,且
,且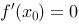 ,则函数
,则函数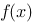 在点
在点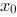 ( )
( )
选项:
A:取得极大值
B:取得极小大值
C:某个邻域内单调增加
D:某个邻域内单调减少
答案: 【取得极大值】
4、 问题:一曲线过(1,0),且具有这样的性质:切线在oy轴上有截距等于切点的极径,则曲线方程为( )
选项:
A: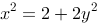
B: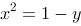
C: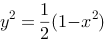
D: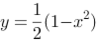
答案: 【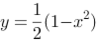 】
】
5、 问题:下列微分方程中为齐次微分方程的是( )
选项:
A: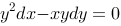
B: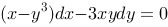
C: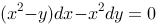
D: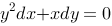
答案: 【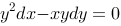 】
】
6、 问题:已知特征根为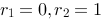 ,则相应的阶数最低的常系数线性齐次微分方程为
,则相应的阶数最低的常系数线性齐次微分方程为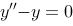
选项:
A:正确
B:错误
答案: 【错误】
7、 问题:微分方程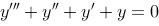 的通解为
的通解为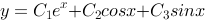
选项:
A:正确
B:错误
答案: 【错误】
8、 问题:设曲线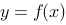 在原点与曲线
在原点与曲线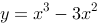 相切,且
相切,且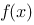 满足关系式:
满足关系式: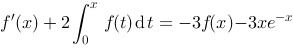 ,则
,则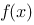 的表达式是
的表达式是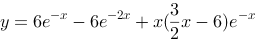 。
。
选项:
A:正确
B:错误
答案: 【正确】
9、 问题:设一阶非齐次线性微分方程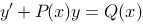 有两个线性无关的解
有两个线性无关的解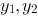 ,若
,若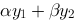 也是该微分方程的解,则应有
也是该微分方程的解,则应有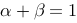
选项:
A:正确
B:错误
答案: 【正确】
10、 问题:微分方程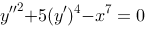 是4阶微分方程
是4阶微分方程
选项:
A:正确
B:错误
答案: 【错误】
【作业】第八章 向量代数与空间解析几何 向量代数与空间解析几何单元作业
1、 问题:设向量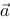 的模为1,
的模为1, 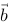 的模为2, 且
的模为2, 且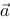 与
与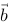 向量的夹角为
向量的夹角为 , 若向量
, 若向量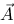
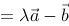 与向量
与向量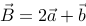 垂直,则系数
垂直,则系数 等于?
等于?
评分规则: 【 由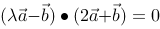 有
有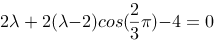
得: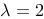
】
2、 问题:求过三个点A(-1,2,3),B(3,2,4),C(1,1,1)的平面方程。
评分规则: 【 法向量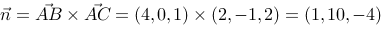
平面方程为:x+10y-4z=7
】
3、 问题:求过点(4,2,3)且平行平面3x-y+z=2及2y-z=3的直线方程。
评分规则: 【 方向向量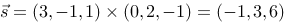
直线方程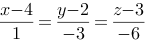
】
4、 问题:平面-x-y+z=4与直线x+1=y=-z+2的位置关系是什么?并说明理由?
评分规则: 【 垂直关系
因为平面法向量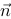 =(-1,-1,1)与直线的方向向量
=(-1,-1,1)与直线的方向向量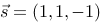 平行.
平行.
】
5、 问题:求向量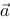 =(2,2,3)与向量
=(2,2,3)与向量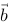 =(1,0,1) 的向量积及点积。
=(1,0,1) 的向量积及点积。
评分规则: 【 向量积为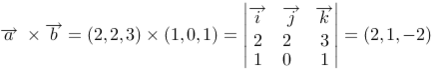
点积为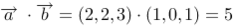
】
6、 问题:求点(1,0,1)到平面x+2y+2z=6的距离。
评分规则: 【 平面法向量
距离为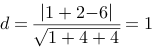
】
7、 问题:设三角形的三个顶点坐标分别为A(1,2, 3), B(2,2, 2), C(3,0,2),求该三角形的面积.
评分规则: 【 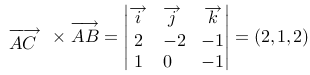
三角形面积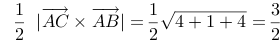
】
8、 问题:垂直平面的向量叫平面的法向量. 零向量是既没有大小也没有方向的量.这两句话是否正确?并说明理由。
评分规则: 【 垂直平面的向量叫平面的法向量是错误的。因为垂直平面的非零向量才叫平面的法向量。
零向量是既没有大小也没有方向的量是错误的。 因为零向量大小为0.
】
9、 问题:求x0z面上的曲线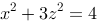 绕z轴旋转一周所得的旋转曲面的方程。
绕z轴旋转一周所得的旋转曲面的方程。
评分规则: 【 绕z轴, z不变,把x换成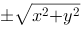
曲面方程为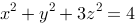 .
.
】
10、 问题:求点P(2,3,1)到直线x=y=z的距离。
评分规则: 【 直线上取一点M(0,0,0), 直线的方向向量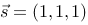 .距离
.距离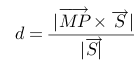
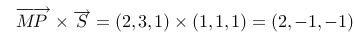 ,距离
,距离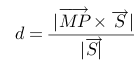
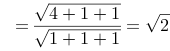 .
.
】
第八章 向量代数与空间解析几何 向量代数与空间解析几何单元测试题
1、 问题:设直线过两点A(1,2,3)和B(3,4,2),则该直线的对称式方程为( )
选项:
A: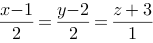
B: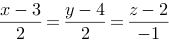
本文章不含期末不含主观题!!
本文章不含期末不含主观题!!
支付后可长期查看
有疑问请添加客服QQ 2356025045反馈
如遇卡顿看不了请换个浏览器即可打开
请看清楚了再购买哦,电子资源购买后不支持退款哦


